Radix Sort
LSD(Least significant digital):排序方式由数值的最右边(低位)开始
MSD(Most significant digital):由数值的最左边(高位)开始。
LSD首先根据个位数的数值,在遍历数据时将它们各自分配到编号0至9的桶(个位数值与桶号一一对应)中。
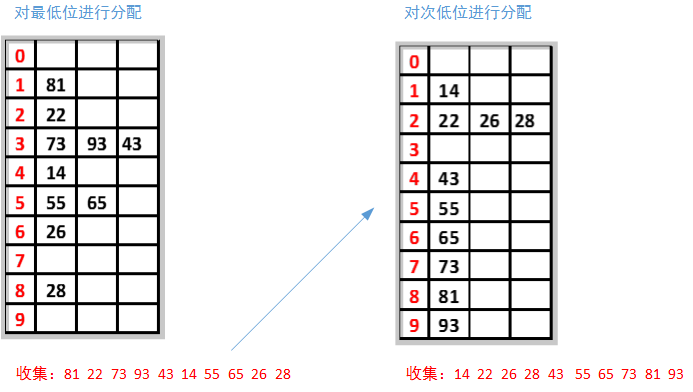
MSD的方式由高位数为基底开始进行分配,但在分配之后并不马上合并回一个数组中,而是在每个“桶子”中建立“子桶”,将每个桶子中的数值按照下一数位的值分配到“子桶”中。在进行完最低位数的分配后再合并回单一的数组中。
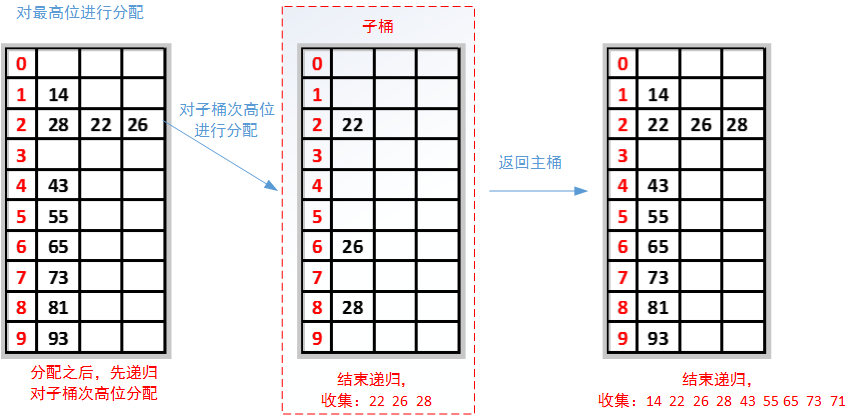
论文导言
MSD基数排序的优点
高效利用内存层次结构
- 通过递归划分数据,子问题规模逐渐缩小,适合利用GPU等处理器的快速本地内存(如共享内存)。当子问题足够小时,可直接在高速内存中完成排序("local-finishing"),减少全局内存访问开销。
提前终止优化
- 如果高位数字已能唯一确定键的顺序,后续低位无需处理,减少不必要的操作(如短字符串排序中前缀差异大的情况)。
性能优势(特定场景)
- 对于数据集分布不均匀或键值差异集中在高位时,MSD可能更快(如[9,18]提到的全局内存排序场景)。
MSD基数排序的缺点
复杂度与开销高
需递归管理多个子问题的分箱(binning),簿记开销大(如维护子问题栈、指针等)。
递归调用可能导致函数调用开销或栈溢出风险。
稳定性问题
- 默认实现不稳定(需额外操作保持稳定性),而稳定性是某些场景(如多键排序)的硬性要求。
分布敏感性能
- 若键值分布集中(如高位数字相同),可能退化为大量小分箱,无法充分利用"local-finishing"优势。
LSD基数排序的优点
简单性与低开销
- 每轮处理一个数字位,只需全局遍历数据一次,无需递归或子问题管理,实现更简单。
稳定排序
- 天然保持稳定性,适合需要保留原始相对顺序的场景(如按多字段排序)。
性能一致性
- 性能与键值分布无关,每轮处理所有数据,适合均匀或不可预测分布的数据。
LSD基数排序的缺点
无法局部优化
- 每轮需处理全部数据,即使部分键已有序,仍需处理所有低位,无法利用高速内存加速。
内存访问效率低
- 频繁全局内存操作(尤其是GPU场景),可能成为瓶颈。
固定迭代次数
- 必须处理所有数字位,即使高位已可确定顺序。
__ballot_sync
_ballot_sync 是 CUDA 中的一种 Warp 级原语(Warp-Level Primitive),用于在 GPU 的线程束(Warp,通常包含 32 个线程)内进行高效的 集体位掩码投票(Collective Bitmask Voting)。它的主要作用是根据线程的 条件判断,生成一个 32 位的掩码(mask),其中每一位代表对应线程的条件是否为真(1=真,0=假)
__global__ void ballot_example(int *data, int *output) {
int tid = threadIdx.x;
int value = data[tid];
// 生成掩码:标记所有 value > 0 的线程
unsigned int mask = __ballot_sync(0xFFFFFFFF, value > 0);
if (tid == 0) {
*output = mask; // 存储掩码(例如 0b1011...)
}
}输出:如果 data = {1, -2, 3, 0},则 mask 可能是 0b0101(线程 0 和 2 满足条件)。
__popc
__popc 是 CUDA 中的一个 内置函数(Intrinsic Function),用于计算一个 32 位或 64 位整数中 置位(1)的位数(Population Count,即 "popcount")。它的作用是高效统计二进制数中 1 的个数.
__global__ void count_ones(int *input, int *output) {
int value = input[threadIdx.x];
int ones = __popc(value); // 统计 value 中 1 的个数
output[threadIdx.x] = ones;
}
int main() {
int input[] = {0xFF, 0xA, 0x1}; // 二进制: 11111111, 1010, 0001
int output[3];
// 调用 GPU 内核
count_ones<<<1, 3>>>(input, output);
cudaDeviceSynchronize();
// output = {8, 2, 1}
} 阿啸
阿啸